二维傅里叶变换(2D Fourier Transforms)可视化
By Long Luo
前言
前几天看了一个介绍 核磁共振成像(MRI) 原理的视频:三维演示磁共振成像(MRI)原理 ,加上自己也曾做过 \(2\) 次核磁共振,一直很好奇其原理,所以花了点时间弄懂了核磁共振成像原理。
在这篇文章我们不详细介绍核磁共振成像原理,只关注其成像部分,也就是根据获取到的空间频率来还原图像,也就是二维傅里叶逆变换(\(\textit{2D Inverse Fourier Transforms}\))。
关于傅里叶变换及傅里叶逆变换,可以参考之前写过的一篇文章:傅里叶变换 。傅里叶变换本质上就是换基,推荐这篇文章:我理解的傅里叶变换 。
一维傅里叶变换(1D Fourier Transform)
对于非周期函数,我们把它的周期看作无穷大。基频 \(\omega_0=\frac{2\pi}{T}\) 则趋近于无穷小,又因为基频相当于周期函数的傅里叶级数中两个相邻频率的差值 \((n+1)\omega_0-n\omega_0\),我们可以把它记作 \(\Delta\omega\) 或者微分 \(d\omega\)。\(n\omega_0\) 则相当于连续变量 \(\omega\)。这样就得到了针对非周期函数的频谱函数如下:
\[ c_{n}=\frac{\Delta\omega}{2\pi}\int_{-\infty}^{+\infty} f(t)e^{-jwt}dt \]
我们会发现这里的 \(c_n\) 是趋于 \(0\) 的。
将它代入 \(f(t)=\sum_{n=-\infty}^{n=+\infty}c_ne^{jn\omega_0t}\)
得到:
\[ f(t)=\sum_{-\infty}^{+\infty}(\frac{\Delta\omega}{2\pi}\int_{-\infty}^{+\infty} f(t)e^{-jwt}dt)e^{j\omega t}=\int_{-\infty}^{+\infty}\frac{1}{2\pi}(\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt)e^{j\omega t}d\omega \]
则非周期函数的傅里叶变换定义为
\[ F(\omega)=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt \]
我们可以发现 \(c_n=\frac{d\omega}{2\pi}F(\omega)\) ,即我们选取了信号幅值在频域中的分布密度 \(F(\omega)\) 来表示傅里叶变换,而不是相应频率的信号幅值大小 \(c_n\) 。因为如果选择后者,那傅里叶变换的函数值就都是无穷小了,这显然对我们没有任何帮助。
我们一般也用频率 \(f\) 来进行傅里叶变换:
\[ F(f)=\int_{-\infty}^{+\infty}f(t)e^{-j2\pi f t}dt \]
在数学上 \(f(t)\) 大多是在时域 \(t\) 上是连续的,但是由于计算机采集信号在时域中是离散的,所以实际应用中的 \(f(t)\) 都是其经采样处理后得到的 \(f_s(t)\) 。
同时,计算机也只能计算出有限个频率上对应的幅值密度,即 \(f\) 也是离散的。
\(\textit{DFT(Discrete Fourier Transform)}\) 也就是 \(t\) 和 \(f\) 都是离散的傅里叶变换。
一维离散傅里叶变换
采样(Sampling)
首先引入冲激函数(也叫 \(\textit{Dirac}\) 函数)的概念。
当 \(t \neq 0\) 时 \(\delta(t)=0\); \(\int_{-\infty}^{+\infty}\delta(t)dt=1\)。
根据它的定义,我们可知 \(\int_{-\infty}^{+\infty}\delta(t-t_0)f(t)dt=f(t_0)\) 。这是 \(\textit{Dirac}\) 函数的重要性质,容易看出,它可以筛选出 \(f(t)\) 在 \(t_0\) 处的函数值,即起到采样的作用。
但是 \(\textit{Dirac}\) 函数一次只能选取一个函数值,所以我们将很多个采样点不同的 \(\textit{Dirac}\) 函数叠加起来,就可以实现时域上的采样了。这样叠加的函数被称为梳状函数,表达式为:
\(\delta_s(t)=\sum_{n=-\infty}^{\infty}\delta(t-nT_s)\) ,其中 \(T_s\) 为采样周期。
将时域上的连续信号与它相乘,即可得到 \(f_s=\sum_{n=-\infty}^{\infty}f(t)\delta(t-nT_s)\) 。
时域离散化计算
对于采样得到的 \(x_s(t)=\sum_{n=-\infty}^{\infty}x(t)\delta(t-nT_s)\) 进行傅里叶变换。
根据傅里叶变换的定义
\[ X(\omega)=\int_{-\infty}^{+\infty}x(t)e^{-j\omega t}dt \]
则 \(X_s(\omega)=\int_{-\infty}^{\infty}(\sum_{n=-\infty}^{\infty}x(t)\delta(t-nT_s))e^{-j\omega t}dt\)
交换积分与求和顺序,得到
\[ X_s(\omega)=\sum_{n=-\infty}^{\infty}\int_{-\infty}^{\infty}x(t)\delta(t-nT_s)e^{-jwt}dt \]
根据 \(\textit{Dirac}\) 函数的筛选特性, \(X_s(\omega)=\sum_{n=-\infty}^{\infty}x(nT_s)e^{-jwnT_s}\)
这样就完成了我们的时域离散化计算。
频域离散化计算
时域离散化得到的结果 \(X_s(\omega)\) 在频域上仍是连续的,而计算机只能求取有限个 \(\omega\) 对应的频谱密度。此外, \(X_s(\omega)\) 中的时域采样次数 \(N\) 为无穷大,实际应用中显然不会进行无穷多次时域采样。
我们首先解决 \(N\) 为无穷大的问题。对于连续信号 \(x(t)\) 进行 \(N\) 次(\(N\) 为有限值)采样,采样周期为 \(T_s\) 。然后对采样得到的信号进行时域上的周期延拓(延拓至正负无穷),这样我们就得到了一个周期为 \(T_0=NT_s\) 的函数。对于周期函数而言,它的频谱密度函数是离散化的,这样我们就成功把频域也进行了离散化。具体计算方法如下:
在一个周期内,离散信号的表达式为 \(x_s(t)=\sum_{n=0}^{N-1}x(t)\delta(t-nT_s)\)
离散信号的傅里叶级数:
\(X(k\omega_0)=\frac{1}{T_0}\int_{0}^{T}(\sum_{n=0}^{N-1}x(t)\delta(t-nT_s))e^{-jkw_0t}dt\) ,其中 \(\omega_0=\frac{2\pi}{T_0}\)。
交换积分和求和次序,
\(X(k\omega_0)=\frac{1}{T_0}\sum_{n=0}^{N-1}\int_{0}^{T}x(t)\delta(t-nT_s)e^{-jk\omega_0t}dt\)
根据狄拉克函数的筛选特性, \(X(k\omega_0)=\frac{1}{T_0}\sum_{n=0}^{N-1}x(nTs)e^{-jk\omega_0nT_s}\)
即 \[ X(k\omega_0)=\frac{1}{NT_s}\sum_{n=0}^{N-1}x(nTs)e^{-j\frac{2\pi}{NT_s}knT_s}=\frac{1}{NT_s}\sum_{n=0}^{N-1}x(nTs)e^{-j\frac{2\pi}{N}kn} \]
为更加简明,令 \(X[k]=X(k\omega_0)T_s\) , \(x[n]=x(nT_s)\),则
\[ X[k]=\frac{1}{N}\sum_{n=0}^{N-1}x[n]e^{-j\frac{2\pi}{N}kn} \]
其中:\(N\) 为采样总点数,\(n\) 为当前采样点,\(x[n]\) 在时域 \(n\) 的信号值,\(k\) 为当前频率值(从 \(0\) Hz 到 \(N-1\) Hz),\(X[k]\) \(\textit{DFT}\) 的结果(是一个复数,包含幅度和相位信息)。
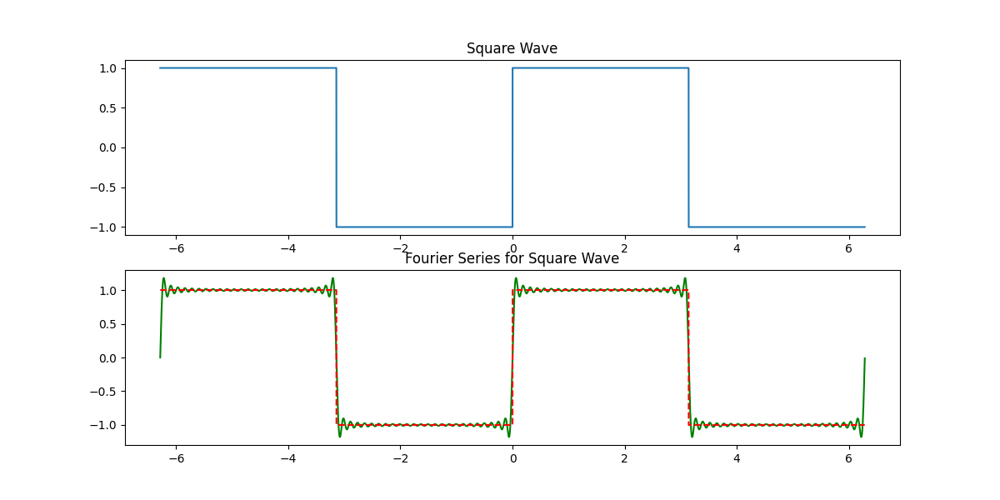
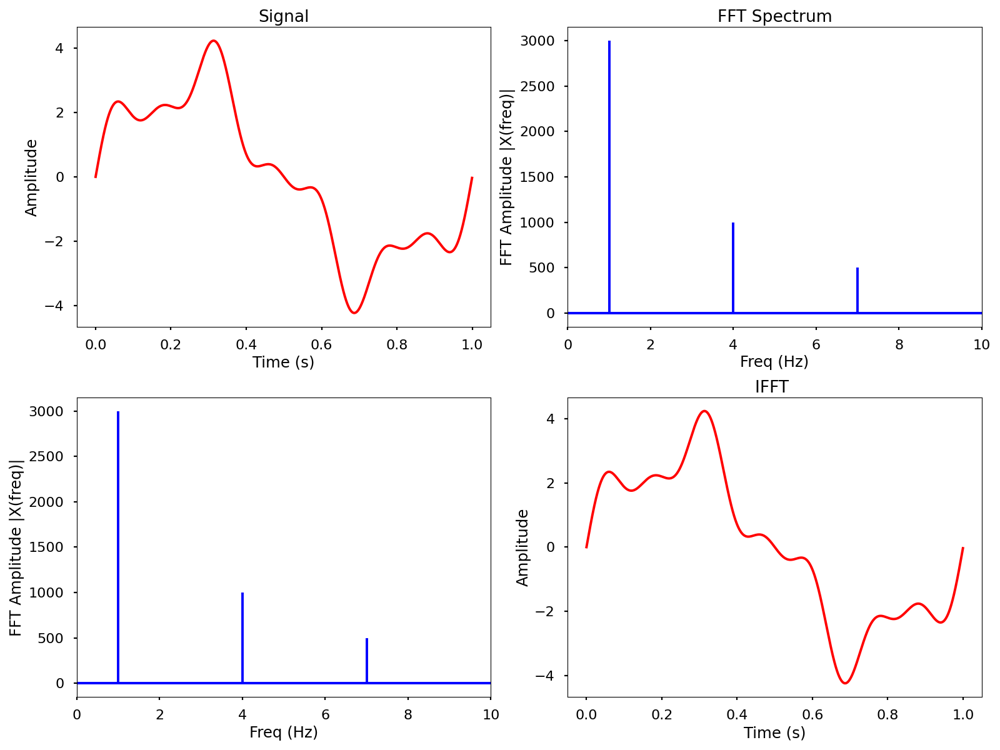
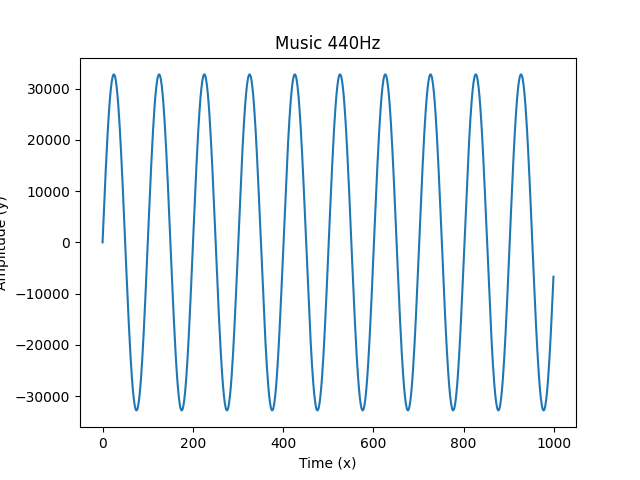
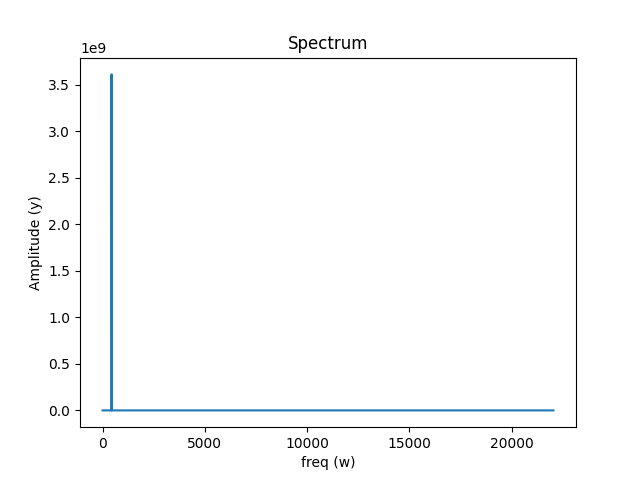
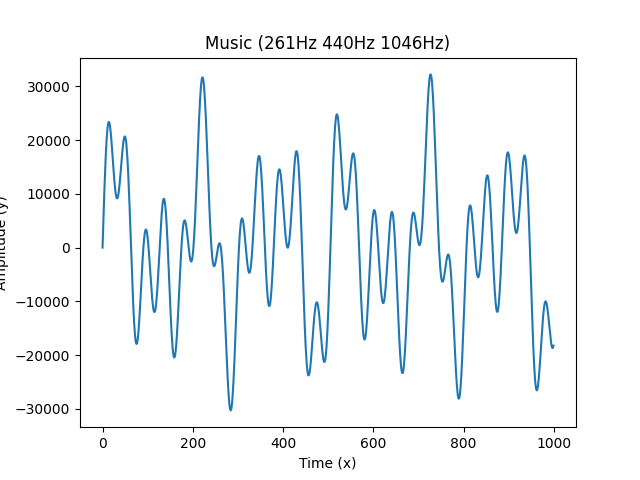
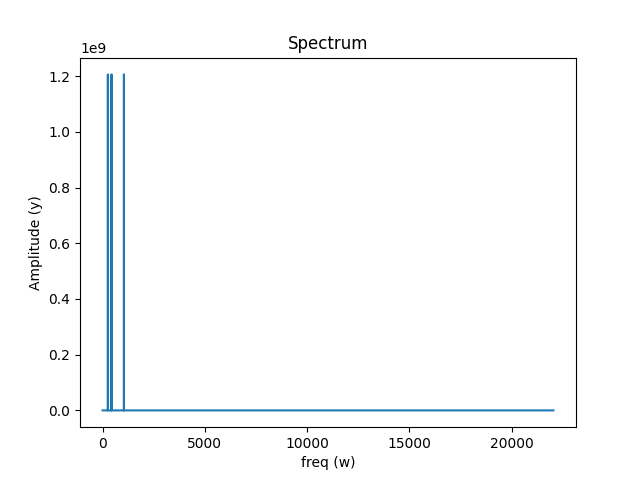
一维傅里叶变换可视化
二维连续傅里叶变换(2D Fourier Transforms)
二维连续傅里叶变换
\[ F(u,v) = \int_{-\infty }^{\infty}\int_{-\infty }^{\infty} f(x,y)e^{-j2\pi(ux+vy)}dxdy \]
二维连续傅里叶逆变换
\[ f(x,y) = \frac{1}{4\pi^2} \int_{-\infty }^{\infty}\int_{-\infty }^{\infty} F(u,v)e^{j2\pi(ux+vy)}dudv \]
二维离散傅里叶变换
二维离散傅里叶变换
\[ F(u,v)=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1}f(x,y)e^{-j2\pi(\frac{ux}{M}+\frac{vy}{N})} \]
二维离散傅里叶逆变换
\[ f(x,y)=\frac{1}{MN}\sum_{x=0}^{M-1} \sum_{y=0}^{N-1}F(u,v)e^{j2\pi(\frac{ux}{M}+\frac{vy}{N})} \]
傅里叶变换特征参数
\[ F(u,v)=R(u,v)+jI(u,v) \]
频谱/幅度谱
\[ |F(u,v)|=\sqrt{R^2(u,v)+I^2(u,v)} \]
\[ P(u,v)=R^2(u,v)+I^2(u,v) \]
相位谱
\[ \psi (u,v)=arctan\frac{I(u,v)}{R(u,v)} \]