[LeetCode][17. Letter Combinations of a Phone Number] 4 Approaches: BF 4 Loops, Backtracking, BFS, Queue with Image Explanation
By Long Luo
This article is the solution 4 Approaches: BF 4 Loops, Backtracking, BFS, Queue with Image Explanation of Problem 17. Letter Combinations of a Phone Number.
Here shows 4 Approaches to slove this problem: Brute Force, Backtracking, BFS and Queue.
Intuition
Take the \(234\) for example, look at the tree: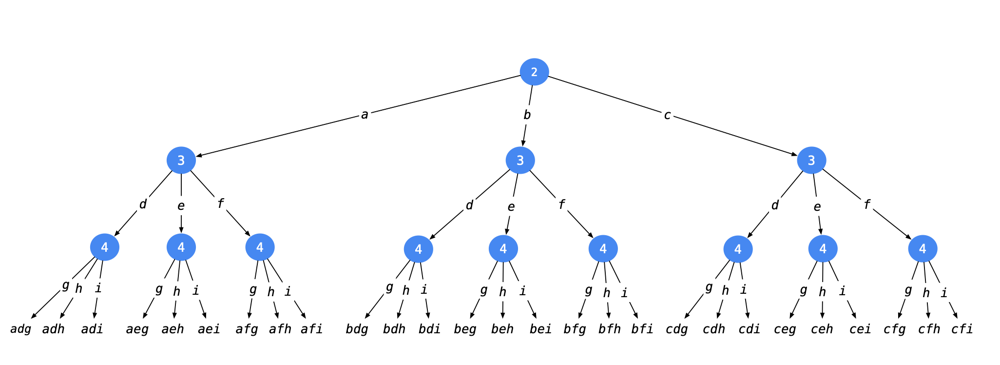
Brute Froce(4 Loops)
Since the \(\textit{digits.length} <= 4\), we can just use the brute force approach \(4\) Loops to search all the possible combinations.
The total states is \(A(n,n)=A(4,4)=4!\). We have to enumerate all these states to get the answer.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46public static List<String> letterCombinations_4Loops(String digits) {
List<String> ans = new ArrayList<>();
if (digits == null || digits.length() == 0) {
return ans;
}
String[] letters = {"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
int len = digits.length();
int[] digitsArr = new int[len];
for (int i = 0; i < len; i++) {
digitsArr[i] = digits.charAt(i) - '0';
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < len; i++) {
sb.append("a");
}
for (int i = 0; i < letters[digitsArr[0] - 2].length(); i++) {
sb.replace(0, 1, letters[digitsArr[0] - 2].charAt(i) + "");
if (len == 1) {
ans.add(sb.substring(0, 1));
}
for (int j = 0; len >= 2 && j < letters[digitsArr[1] - 2].length(); j++) {
sb.replace(1, 2, letters[digitsArr[1] - 2].charAt(j) + "");
if (len == 2) {
ans.add(sb.toString());
}
for (int k = 0; len >= 3 && k < letters[digitsArr[2] - 2].length(); k++) {
sb.replace(2, 3, letters[digitsArr[2] - 2].charAt(k) + "");
if (len == 3) {
ans.add(sb.toString());
}
for (int l = 0; len >= 4 && l < letters[digitsArr[3] - 2].length(); l++) {
sb.replace(3, 4, letters[digitsArr[3] - 2].charAt(l) + "");
ans.add(sb.toString());
}
}
}
}
return ans;
}
Analysis
- Time Complexity: \(O(4^N)\)
- Space Complexity: \(O(N)\)
Backtracking
For the first number, there are \(3\) options, and \(3\) options for the second number and so on.
The combinations from the first to the last will expand into a recursive tree.
When the index reaches the end of digits, we get a combination, and add it to the result, end the current recursion. Finally we will get all the combinations.
1 | public static List<String> letterCombinations(String digits) { |
Analysis
- Time Complexity: \(O(3^M \times 4^N)\)
- Space Complexity: \(O(3^M \times 4^N)\)
BFS
- At the beginning, it is an empty string.
- The new layer is obtained by adding characters at the end of the previous layer.
- After the new layer is obtained, the previous layer is not used.
1 | public static List<String> letterCombinations_bfs(String digits) { |
Analysis
- Time Complexity: \(O(3^M \times 4^N)\)
- Space Complexity: \(O(3^M \times 4^N)\)
Queue
Look at the gif, it’s easy to understand the queue solution.
First we enqueue each letter of the first number in the digits, and then combine the dequeued element with each letter of the second number and enqueue to the queue.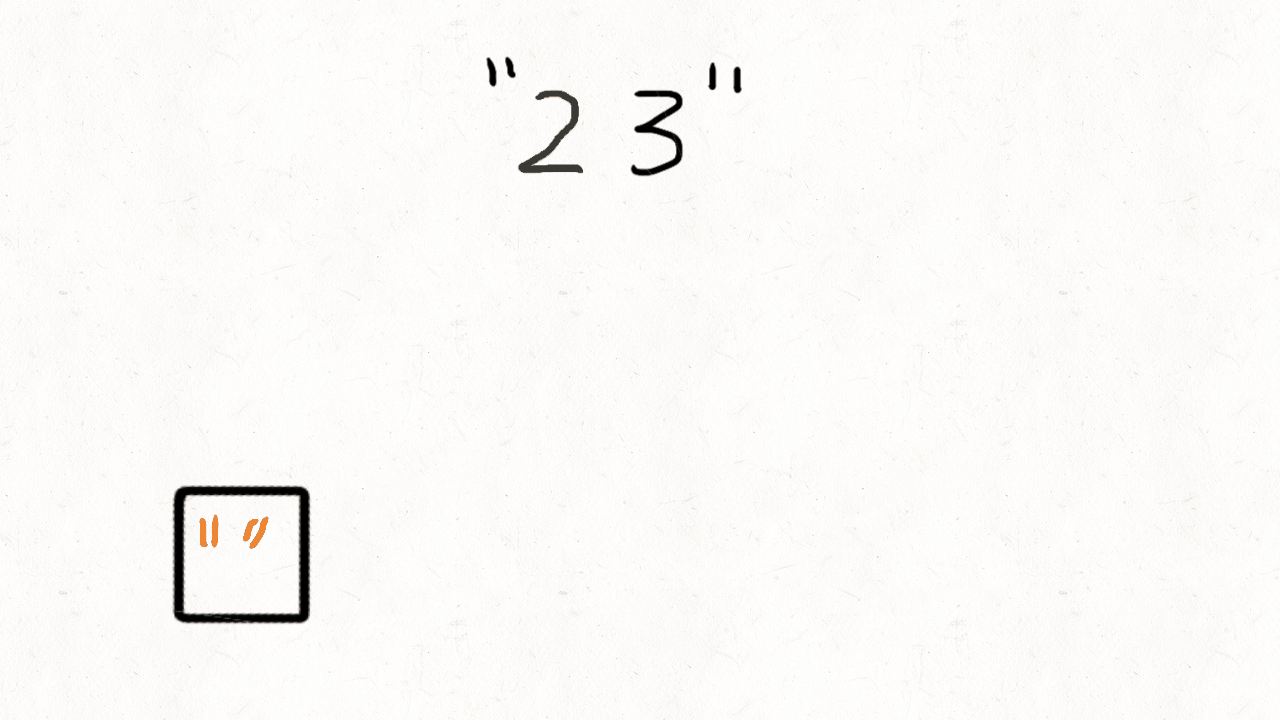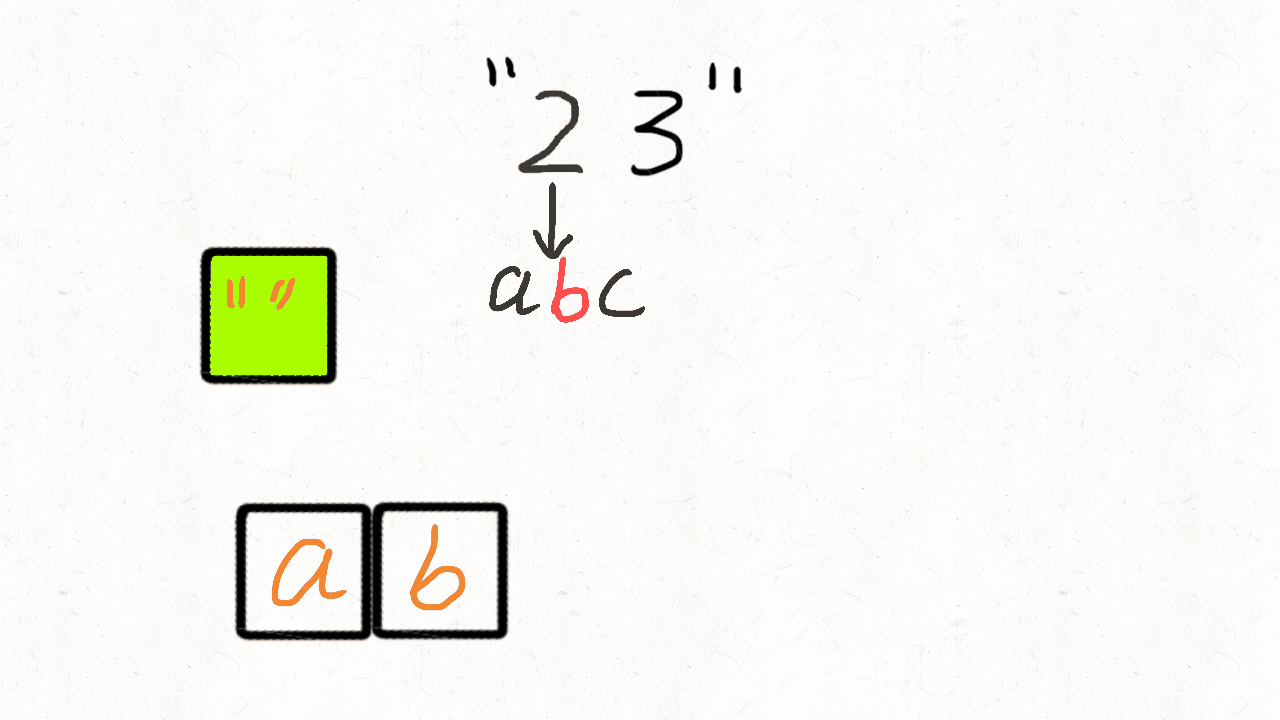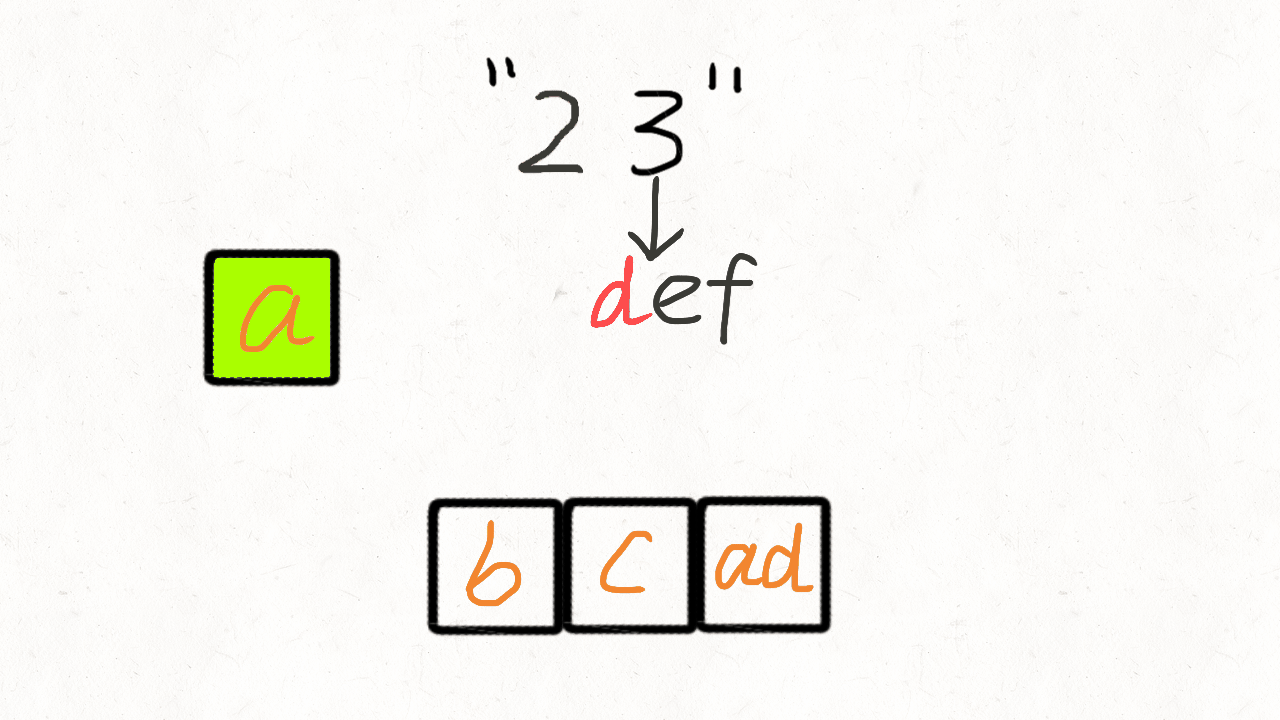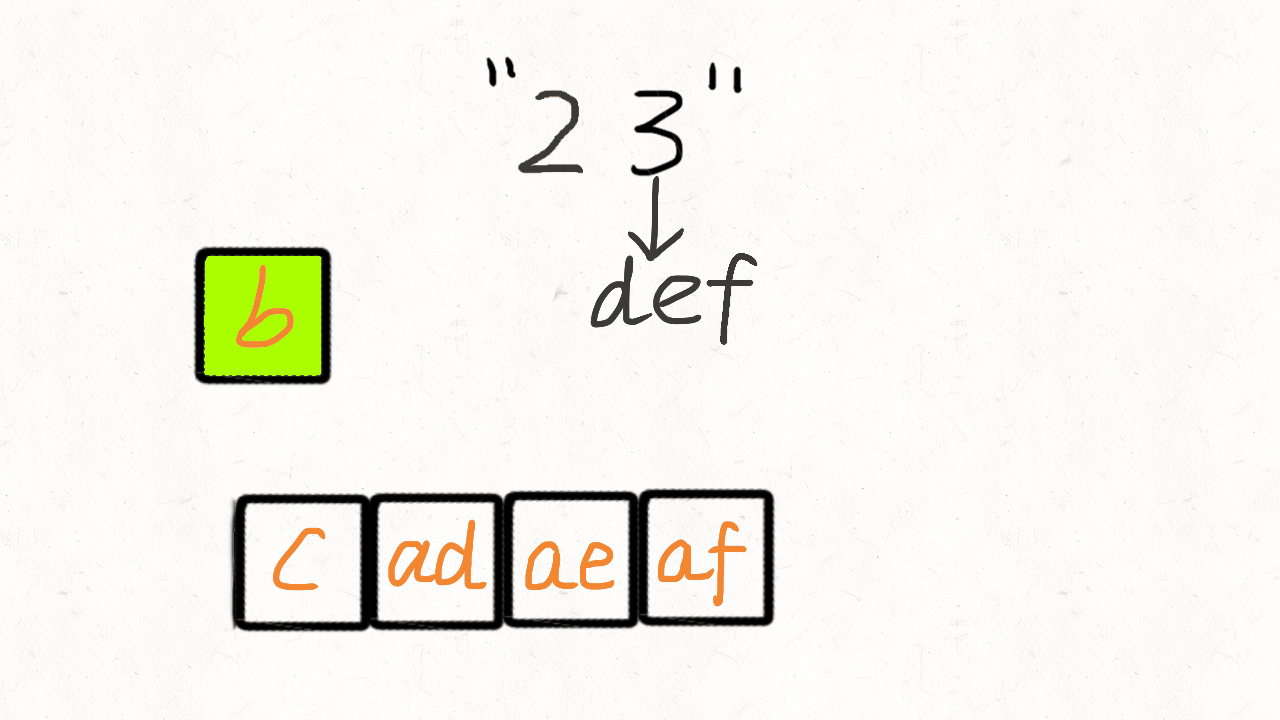
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27public static List<String> letterCombinations_queue(String digits) {
if (digits == null || digits.length() == 0) {
return new ArrayList<>();
}
int len = digits.length();
String[] letters = {"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
Queue<String> queue = new LinkedList<>();
int[] digitsArr = new int[len];
for (int i = 0; i < len; i++) {
digitsArr[i] = digits.charAt(i) - '0';
}
queue.offer("");
for (int i = 0; i < len; i++) {
String letter = letters[digitsArr[i] - 2];
int size = queue.size();
for (int j = 0; j < size; j++) {
String temp = queue.poll();
for (char ch : letter.toCharArray()) {
queue.offer(temp + ch);
}
}
}
return new ArrayList<>(queue);
}
Analysis
- Time Complexity: \(O(3^M \times 4^N)\)
- Space Complexity: \(O(3^M \times 4^N)\)
All suggestions are welcome. If you have any query or suggestion please comment below. Please upvote👍 if you like💗 it. Thank you:-)
Explore More Leetcode Solutions. 😉😃💗