快速傅里叶变换(FFT)算法的实现及优化

发表于 更新于 分类于 Waline： 阅读次数： 本文字数： 6.5k 阅读时长 ≈ 6 分钟

By Long Luo

之前的文章 快速傅里叶变换(FFT)算法 详细介绍了 \(\textit{FFT}\) 的具体实现，也实现了分治版的 \(\textit{FFT}\)。

分治版 \(\textit{FFT}\) 代码很容易理解，但递归会消耗 \(O(logn)\) 的栈空间，同时代码实现中还有很多优化空间，这篇文章我们就来优化 \(\textit{FFT}\) 下的实现。

Cooley–Tukey FFT Algorithm

\(\textit{Cooley–Tukey FFT Algorithm}\) 1 通过使用分治算法2 实现将复杂问题简单化。

FFT 分治过程

FFT

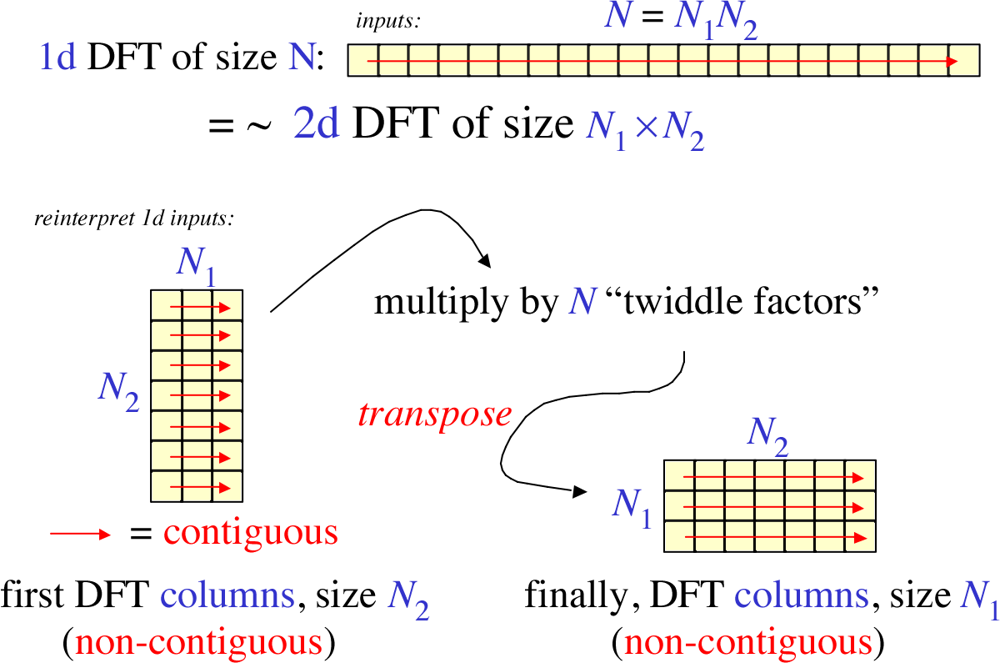
具体操作流程可以分为 \(3\) 步：

  1. Divide：按照奇偶分为 \(2\) 个子问题。
  2. Conquer：递归处理 \(2\) 个子问题
  3. Combine：合并 \(2\) 个子问题。

蝴蝶操作

分治的前 \(2\) 步之前已经详细讲述过了，第 \(3\) 步合并操作是通过蝴蝶操作(Butterfly Operations)来实现的，其示意图如下所示：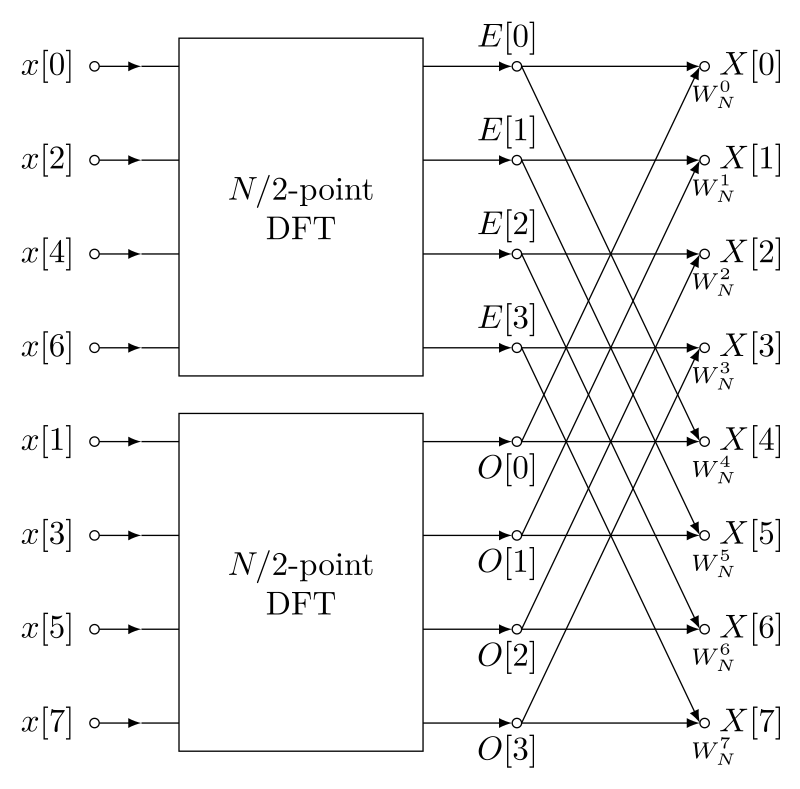

Butterfly Operations

蝴蝶操作可能会让人看了一头雾水，不过没关系，我们一步一步来，彻底弄懂她！

空间优化

回顾之前的 递归版代码 ，在合并这一步，这一层有 \(n\) 项需要处理，我们新建了一个数组 \(y(n)\)，这是为什么呢？

我们可以复用之前的 \(y_e\) 或 \(y_o\) 数组以降低空间复杂度吗？

先看下合并需要做的操作：

\[ y(k) = y_e(k) + \omega_{n}^{k} \cdot y_o(k+\frac{n}{2}) \]

\[ y(k + \frac{n}{2}) = y_e(k) - \omega_{n}^{k} \cdot y_o(k+\frac{n}{2}) \]

很明显，我们如果复用 \(y_e\) 或 \(y_o\) 数组的话，那 \(y(k)\) 和 \(y(k + \frac{n}{2})\) 至少有一个数据会受影响，所以我们需要额外的 \(y(n)\) 数组来存储数据。

那么有没有办法来做到复用 \(y_e\) 或 \(y_o\) 数组呢？

当然可以！

我们只要将修改下合并顺序，加入一个临时变量 \(t=\omega_{n}^{k} \cdot y_e(k+\frac{n}{2})\) ，合并过程就可以在原数组中进行：

\[ cd \; t = \omega_{n}^{k} \cdot y_e(k+\frac{n}{2}) \]

\[ y_e(k+\frac{n}{2}) = y_e(k) - t \]

\[ y_e(k) = y_e(k)+t \]

这样就可以原地进行了，不再需要额外数组。

位逆序置换

在分治过程中，每一次都会把整个多项式的奇数次项和偶数次项系数分开，一直分到只剩下一个系数。因此，如果我们可以先模拟递归把这些系数在原数组中交换位置，把每个系数都放在最终的位置上，再一步一步向上合并。

以 \(8\) 项多项式为例，模拟递归拆分的过程：每一次分组情况如下图：

  • 初始序列为 \(\{x_0, x_1, x_2, x_3, x_4, x_5, x_6, x_7\}\)

  • 一次二分之后 \(\{x_0, x_2, x_4, x_6\}, \{x_1, x_3, x_5, x_7\}\)

  • 两次二分之后 \(\{x_0, x_4\}, \{x_2, x_6\}, \{x_1, x_5\}, \{x_3, x_7\}\)

  • 三次二分之后 \(\{x_0\} \{x_4\} \{x_2\} \{x_6\} \{x_1\} \{x_5\} \{x_3\} \{x_7\}\)

拆分前后数组位置变化情况如下：

Index
原序列:01234567
原数组:000001010011100101110111
后序列：04261537
后数组:000100010110001101011111

发现规律了没？

二进制翻转

后序列是原序列的二进制翻转。原序列每个数用二进制表示，然后把二进制翻转对称一下，就是最终那个位置的下标。比如 \(x_1=(001)_{2}\) ，翻转是 \(4=(100)_2\) 。这个变换为位逆序置换（bit-reversal permutation，也就是蝴蝶变换）。

根据它的定义，我们可以在 \(O(nlog n)\) 的时间内求出每个数变换后的结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/*
 * 进行 FFT 和 IFFT 前的反置变换
 * 位置 i 和 i 的二进制反转后的位置互换
 * len 必须为 2 的幂
 */
void change(vector<complex<double>>& y, int len) {
    int k;
    for (int i = 1, j = len / 2; i < len - 1; i++) {
        if (i < j) {
            swap(y[i], y[j]);
        }

        // 交换互为小标反转的元素，i<j 保证交换一次
        // i 做正常的 + 1，j 做反转类型的 + 1，始终保持 i 和 j 是反转的
        k = len / 2;
        while (j >= k) {
            j = j - k;
            k = k / 2;
        }

        if (j < k) {
            j += k;
        }
    }
}

反向二进制加法

实际上，位逆序变换相当于一个反向二进制加法，因为原序列是每次从二进制右端加 \(1\) 地递增，翻转后，就相当于每次从二进制左端加 \(1\)，这样的话就可以 \(O(n)\) 从小到大递推实现。

我们来推理下如何实现3：

设 \(len=2^k\)，其中 \(k\) 表示二进制数的长度，设 \(R(x)\) 表示长度为 \(k\) 的二进制数 \(x\) 翻转后的数（高位补 \(0\)）。我们要求的是： \(R(0),R(1),\cdots,R(n-1)\)。

  1. \(R(0)=0\)。

  2. 从小到大求 \(R(x)\)。

待求的问题可以分为 \(2\) 步:

  1. 求最后一位之前的二进制数的倒置结果；

  2. 把被抹去的原来的最后一位放回结果的第一位。

对于第一步：

最后一位前面的二进制数取反后是多少？因为我们进行位逆序置换的过程是从 \(0\) 到 \(len\) 的，而求最后一位前面的二进制数也就等于把所需要求的数的右移一位（除以 \(2\)），所以最后一位前面的二进制数的倒置就是你在之前已经求过的 \(R(x >> 1) = R\left(\left\lfloor \dfrac{x}{2} \right\rfloor\right)\)。

但我们在进行位逆序置换时，会将一个数的二进制表示前面的 \(0\) 补齐，使得其长度等于 \(k\)，例如 \(k=5\)，\((12)_10=(1100)_2\) 补齐至 \((01100)_2\)，再进行位逆序置换得到 \((00110)_2\)。这样我们得到的 \(R(x/2)\) 其实与我们所求的最后一位前面的二进制数的倒置是不一致的，我们要求 \((1100)_2\) 的倒置，但求得的却是 \((01100)_2\) 的倒置，也就是说我们在 \(x\) 的最前面多了一位，逆置之后也就是在结果的最后多了一位，所以我们第一个问题的结果不是 \(R(x >> 1)\) 而是 \(R(x >> 1) >> 1\)， 也就是通过将原来的结果右移一位消去补上去的那一位。

解决了第一步，对于第二步来说就非常简单了。如果之前的个位是 \(0\)，翻转之后最高位就是 \(0\)；如果个位是 \(1\)，则翻转后最高位是 \(1\)，也就是结果再加上 \(\dfrac{len}{2}=2^{k-1}\)。

综上：

\[ R(x)=\left\lfloor \frac{R\left(\left\lfloor \frac{x}{2} \right\rfloor\right)}{2} \right\rfloor + (x\bmod 2)\times \frac{len}{2} \]

举个例子来说明下：

设 \(k=5\) ，\(len=(32)_{10}=(100000)_2\) ，假设待翻转的数是 \((25)_{10}=(11001)_2\) ：

  1. 考虑 \((12)_{10}=(1100)_2\) ，我们知道 \(R((1100)_2)=R((01100)_2)=(00110)_2\) ，再右移一位就得到了 \((3)_{10}=(00011)_2\) ；

  2. 考虑个位，如果是 \(1\) ，它就要翻转到数的最高位，即翻转数加上 \((16)_{10}=(10000)_2=2^{k-1}\) ，如果是 \(0\) 则不用更改；

  3. 最终结果是 \((00011)_2 + (10000)_2 = (19)_{10}\)

位逆序变换代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 同样需要保证 len 是 2 的幂
// 记 rev[i] 为 i 翻转后的值
void bitReverse(vector<complex<double>> &y, int len) {
    vector<int> rev(len);

    rev[0] = 0;
    for (int i = 1; i < len; i++) {
        // 最后一位之前的部分
        rev[i] = rev[i >> 1] >> 1;
        if (i & 1) {  // 如果最后一位是 1，需要再加上 len/2
            rev[i] |= len >> 1;
        }
    }

    for (int i = 0; i < len; ++i) {
        if (i < rev[i]) {  // 保证每对数只翻转一次
            swap(y[i], y[rev[i]]);
        }
    }

    return;
}

FFT 迭代版

通过位逆序置换，我们可以用迭代替代分治递归 \(\textit{FFT}\) ，优化 \(\textit{FFT}\) 性能。

回放原先的递归过程，方便理解(从下往上倒推)：

\[ \left \{ a_0,a_1,a_2,a_3,a_4,a_5,a_6,a_7 \right \} \]

\[ \left \{ a_0,a_2,a_4,a_6 \right \}, \left\{ a_1,a_3,a_5,a_7 \right \} \]

\[ \left \{a_0,a_4 \right \},\left \{ a_2,a_6 \right \},\left\{ a_1,a_5 \right \},\left\{ a_3,a_7 \right \} \]

\[ \left\{ a_0 \right \},\left\{ a_4 \right \},\left\{ a_2 \right \},\left\{ a_6 \right \},\left\{ a_1 \right \},\left\{ a_5 \right \},\left\{ a_3 \right \},\left\{ a_7 \right \} \]

这其中有三层循环，第一层循环表示当前需要合并的多项式的长度：从每段长度为 \(1\) 合并为 \(2\)，而后 \(4\) 直到最大：

从

\[ \underbrace{\left\{a_0,a_4 \right \}}_{len=2},\underbrace{\left\{ a_2,a_6 \right \}}_{len=2},\underbrace{\left\{a_1,a_5 \right \}}_{len=2},\underbrace{\left\{a_3,a_7 \right \} }_{len=2} \]

\(len<<1\) 到

\[ \underbrace{\left\{ a_0,a_2,a_4,a_6 \right \}}_{len=4}, \underbrace{\left\{ a_1,a_3,a_5,a_7 \right \}}_{len=4} \]

以此类推：

1
2
3
for (int len = 2; len <= n; len <<= 1) {

}

之后我们需要标记每个多项式的开头( \(j+=len\) )：

\[ \mathop{\uparrow}\limits_{j=0} \underbrace{ \left\{a_0,a_4 \right \} }_{len=2},\mathop{\uparrow}\limits_{j+=len}\underbrace{\left\{a_2,a_6 \right \}}_{len=2},\mathop{\uparrow}\limits_{j+=len}\underbrace{\left\{ a_1,a_5 \right \}}_{len=2},\mathop{\uparrow}\limits_{j+=len}\underbrace{\left\{ a_3,a_7 \right \}}_{len=2} \]

同时因为每个多项式对应的根不一样, 因此我们需要在两层循环之间定义单位根 \(\omega_n\) 和 \(\omega\)，不断乘以 \(\omega_n\) 切换根的数值。

1
2
3
4
5
6
7
8
9
double ang = 2 * PI / n * (invert ? -1 : 1);
complex<double> wn(cos(ang), sin(ang)); // omega为第一个n次复根,
complex<double> w(1, 0);   // curr为第零0个n次复根, 即为 1

for (int i = 2; i <= n; i <<= 1) {
    for (int j = 0; j < n; j += i) {

    }
}

那么第三重循环的实现就很简单了：

1
2
3
4
5
6
7
8
9
10
11
for (int i = 2; i <= n; i <<= 1) {
    for (int j = 0; j < n; j += i) {
        for (int k = j; k < j + i / 2; k++) {
            complex<double> t = a[k];
            complex<double> b = w * a[k + i / 2];
            a[k] = t + b;
            a[k + i / 2] = t - b;
            w *= wn;
        }
    }
}

\(\textit{FFT}\) 迭代版代码最终实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * FFT Iteration 实现
 *
 * @param a
 * @param invert true means IFFT, else FFT
 * @return y
 */
void FFT(vector<complex<double>> &a, bool invert) {
    int n = a.size();

    if (n == 1) {
        return;
    }

    bitReverse(a);

    for (int len = 2; len <= n; len <<= 1) {
        double ang = 2 * PI / len * (invert ? -1 : 1);
        complex<double> wlen(cos(ang), sin(ang));

        for (int i = 0; i < n; i += len) {
            complex<double> w(1, 0);
            for (int j = 0; j < len / 2; j++) {
                complex<double> u = a[i + j];
                complex<double> v = w * a[i + j + len / 2];
                a[i + j] = u + v;
                a[i + j + len / 2] = u - v;
                w *= wlen;
            }
        }
    }
	
    if (invert) {
        for (auto &x : a) {
            x /= n;
        }
    }	
}

应用及实践

43. 字符串相乘

POLYMUL - Polynomial Multiplication4

参考资料

  1. Wiki: Cooley–Tukey FFT algorithm↩︎

  2. Wiki: Divide-and-conquer algorithm↩︎

  3. OI Wiki: 快速傅里叶变换↩︎

  4. Algorithm: Fast Fourier Transform↩︎