[LeetCode][1721. Swapping Nodes in a Linked List] 3 Approaches: Swapping Values and Swapping Nodes with Image Explanation

发表于 更新于 分类于 Waline： 阅读次数： 本文字数： 3.3k 阅读时长 ≈ 3 分钟

By Long Luo

This article is the solution 3 Approaches: Swapping Values and Swapping Nodes with Image Explanation of Problem 1721. Swapping Nodes in a Linked List.

Here shows 3 Approaches to slove this problem: ArrayList and Two Pointers.

Intuition

Since the \(\texttt{ListNode}\) only contain values, we can just just swap the values of two nodes. It’s very easy. All we need to do is to find these two nodes and swap their values.

If we swap nodes, it will be more difficult than swap values.

ArrayList(Swapping Values)

We can use an \(\texttt{ArrayList}\) to record all the nodes of the linked list. We can just swap the values of two nodes.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
  // BF List time: O(n) space: O(n)
  public static ListNode swapNodes_bf_list(ListNode head, int k) {
      ListNode pNode = head;
      List<ListNode> nodeList = new ArrayList<>();
// store these nodes.
      while (pNode != null) {
          nodeList.add(pNode);
          pNode = pNode.next;
      }

// swap their values.
      int len = nodeList.size();
      int temp = nodeList.get(k - 1).val;
      nodeList.get(k - 1).val = nodeList.get(len - k).val;
      nodeList.get(len - k).val = temp;

      return head;
  }

Analysis

  • Time Complexity: \(O(n)\)
  • Space Complexity: \(O(n)\)

Two Pointers(Swapping Values)

The space complexity of Method \(1\) is \(O(n)\). We can use Two Pointers to make it to \(O(1)\).

Just follow the bellow steps:

  1. Find the \(k-th\) node from the front which is left.
  2. Make left node as the current node, right node from the front, when the current node reach end, right node is just the \(k-th\) last element.
  3. Swap their values.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
  // Two Pointers time: O(n) space: O(1)
  public static ListNode swapNodes_tp(ListNode head, int k) {
      ListNode left = head;
      ListNode right = head;
      int cnt = 0;
// find the k-th node
      while (left != null) {
          cnt++;
          if (cnt == k) {
              break;
          }
          left = left.next;
      }

// find the k-th last element
      ListNode pNode = left;
      while (pNode.next != null) {
          pNode = pNode.next;
          right = right.next;
      }

// swap their values.
      int temp = left.val;
      left.val = right.val;
      right.val = temp;

      return head;
  }

Analysis

  • Time Complexity: \(O(n)\)
  • Space Complexity: \(O(1)\)

Two Pointers(Swapping Nodes)

In fact, Swapping Nodes will be more difficult. There are some corner cases.

We need to store both the previous and current nodes of these two nodes, denoted them as \(\textit{preLeft}\) and \(\textit{preRight}\).

However, here are 3 corner cases, as the bellow image shows.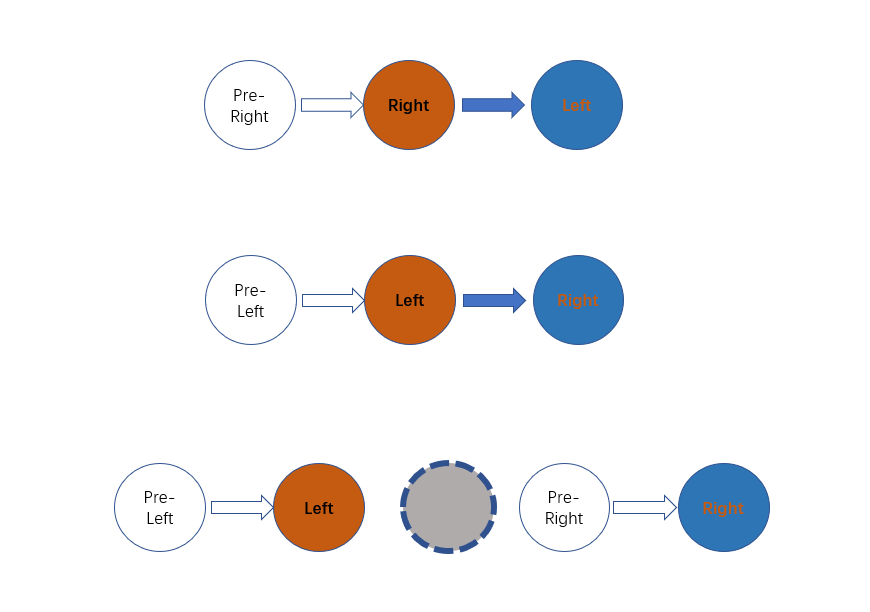

Swap Nodes

We must handle these 3 cases.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
  // Two Pointers Swap Nodes time: O(n) space: O(1)
  public static ListNode swapNodes_tp_swapNode(ListNode head, int k) {
      ListNode dummyNode = new ListNode(0);
      dummyNode.next = head;
      ListNode preLeft = dummyNode;
      ListNode left = head;
      ListNode preRight = dummyNode;
      ListNode right = head;

// find the k-th node
      for (int i = 1; i < k; i++) {
          preLeft = preLeft.next;
          left = left.next;
      }

// find the k-th last node
      ListNode curNode = left;
      while (curNode.next != null) {
          curNode = curNode.next;
          preRight = preRight.next;
          right = right.next;
      }

      ListNode tempNode = left.next;
// if right is the left neighbor of left
      if (preLeft == right) {
          preRight.next = left;
          left.next = right;
          right.next = tempNode;
      } else if (left == preRight) { // if left is the right neighbor of left
          left.next = right.next;
          preLeft.next = right;
          right.next = left;
      } else { // common cases.
          preLeft.next = right;
          left.next = right.next;
          preRight.next = left;
          right.next = tempNode;
      }

      return dummyNode.next;
  }

Analysis

  • Time Complexity: \(O(n)\)
  • Space Complexity: \(O(1)\)

All suggestions are welcome. If you have any query or suggestion please comment below. Please upvote👍 if you like💗 it. Thank you:-)

Explore More Leetcode Solutions. 😉😃💗