5分钟掌握矩阵乘法的Strassen算法

发表于 2019-06-21 更新于 2023-11-14 分类于 Data Structures and Algorithms Waline：阅读次数：本文字数： 6.4k 阅读时长 ≈ 6 分钟

By Long Luo

机器学习中需要训练大量数据，涉及大量复杂运算，例如卷积、矩阵等。这些复杂运算不仅多，而且每次计算的数据量很大，如果能针对这些运算进行优化，可以大幅提高性能。

一、矩阵乘法

假设 \(A\) 为 \(m \times p\) 的矩阵，\(B\) 为 \(p \times n\) 的矩阵，那么称 \(m \times n\) 的矩阵 \(C\) 为矩阵 \(A\) 与 \(B\) 的乘积，记作 \(C = AB\)，称为矩阵积（\(\textit{Matrix Product}\)）。

其中矩阵 \(C\) 中的第 \(i\) 行第 \(j\) 列元素可以表示为：

\[ (AB)_{ij} = \sum_{k=1}^{p}{a_{ik}b_{kj}} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots + a_{ip}b_{pj} \]

如下图所示：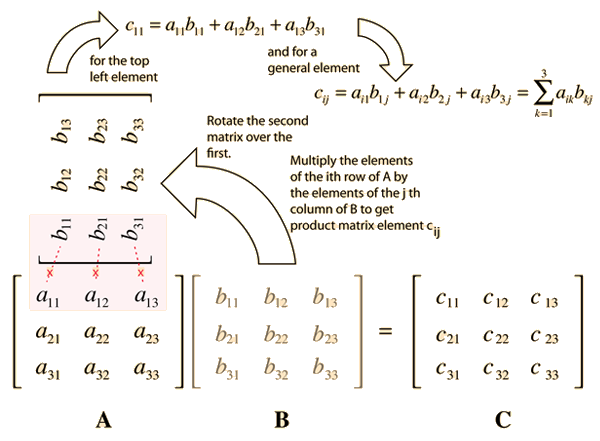

@Figure 1. Matrix Multiplication | center

假如在矩阵 \(A\) 和矩阵 \(B\) 中，\(m=p=n=N\)，那么完成 \(C=AB\) 需要多少次乘法呢？

对于每一个行向量 \(r\) ，总共有 \(N\) 行；
对于每一个列向量 \(c\) ，总共有 \(N\) 列；
计算它们的内积，总共有 \(N\) 次乘法计算。

综合可以看出，矩阵乘法的算法复杂度是：\(O(N^3)\)。

二、Strassen算法

那么有没有比 \(O(N^{3})\) 更快的算法呢？

1969年，Volker Strassen 提出了第一个算法时间复杂度低于 \(O(N^{3})\) 矩阵乘法算法，算法复杂度为 \(O(n^{log_{2}^{7}})=O(n^{2.807})\) 。从下图可知，\(\textit{Strassen}\) 算法只有在对于维数比较大的矩阵( \(N > 300\) ) ，性能上才有很大的优势，可以减少很多乘法计算。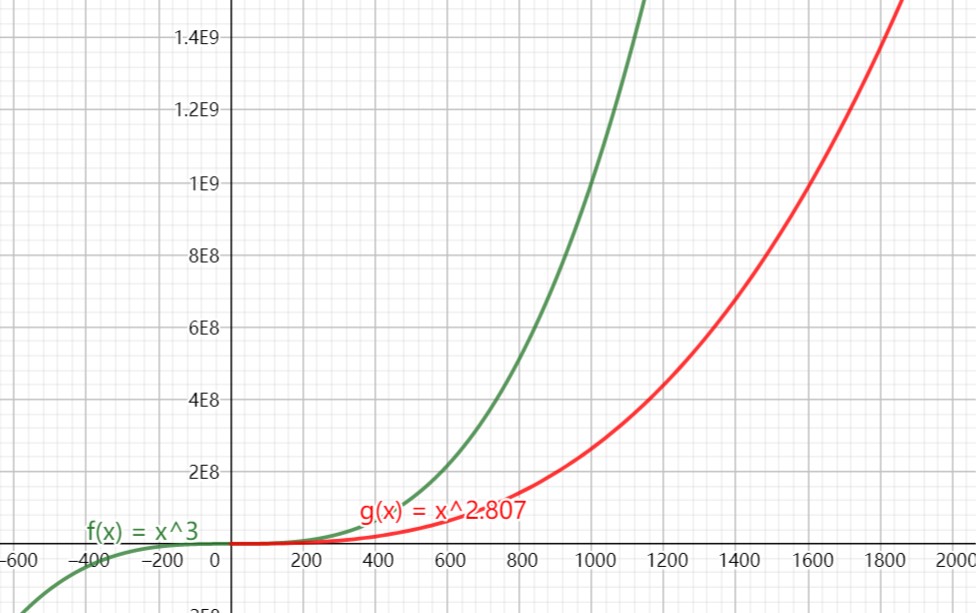

\(\textit{Strassen}\) 算法证明了矩阵乘法存在时间复杂度低于 \(O(N^{3})\) 的算法的存在，后续学者不断研究发现新的更快的算法，截止目前时间复杂度最低的矩阵乘法算法是 Coppersmith-Winograd 方法的一种扩展方法，其算法复杂度为 \(O(n^{2.375})\) 。

三、Strassen原理详解

假设矩阵 \(A\) 和矩阵 \(B\) 都是 \(N \times N (N = 2^{n})\) 的方矩阵，求 \(C = AB\) ，如下所示：

\[ \begin{aligned} A = \left [\begin{matrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{matrix} \right] \\ B = \left [\begin{matrix} B_{11} & B_{12} \\ B_{21} & B_{22} \\ \end{matrix} \right] \\ C = \left [\begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \\ \end{matrix} \right] \end{aligned} \]

其中

\[ \begin{bmatrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{bmatrix} = \begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix} \cdot \begin{bmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{bmatrix} \]

矩阵 \(C\) 可以通过下列公式求出：

\[ \begin{aligned} C_{11} = A_{11} \cdot B_{11} + A_{12} \cdot B_{21} \\ C_{12} = A_{11} \cdot B_{12} + A_{22} \cdot B_{21} \\ C_{21} = A_{21} \cdot B_{11} + A_{22} \cdot B_{21} \\ C_{22} = A_{21} \cdot B_{12} + A_{22} \cdot B_{22} \\ \end{aligned} \]

从上述公式我们可以得出，计算 \(2\) 个 \(n \times n\) 的矩阵相乘需要 \(2\) 个 \(\frac{n}{2} \times \frac{n}{2}\) 的矩阵 \(8\) 次乘法和 \(4\) 次加法。

我们使用 \(T(n)\) 表示 \(n \times n\) 矩阵乘法的时间复杂度，那么我们可以根据上面的分解得到下面的递推公式：

\[ T(n) = 8 \times T(\frac{n}{2}) + O(n^{2}) \]

其中： 1. \(8T(\frac{n}{2})\) 表示 \(8\) 次矩阵乘法，而且相乘的矩阵规模降到了 \(\frac{n}{2}\)。 2. \(O(n^{2})\) 表示 \(4\) 次矩阵加法的时间复杂度以及合并矩阵 \(C\) 的时间复杂度。

最终可计算得到 \(T(n)=O(n^{log_{2}^{8}})=O(n^{3})\) 。

可以看出每次递归操作都需要 \(8\) 次矩阵相乘，而这正是瓶颈的来源。相比加法，矩阵乘法是非常慢的，于是我们想到能不能减少矩阵相乘的次数呢？

答案是当然可以！！！

\(\textit{Strassen}\) 算法正是从这个角度出发，实现了降低算法复杂度！

Strassen实现步骤

实现步骤可以分为以下 \(4\) 步： 1. 按上述方法将矩阵 \(A, B, C\) 分解（花费时间 \(O(1)\)。 2. 如下创建 \(10\) 个 \(\frac{n}{2} \times \frac{n}{2}\) 的矩阵 \(S_1, S_2, \cdots, S_{10}\) (花费时间 \(O(n^2)\)。

\[ \begin{aligned} S_1 = B_{12} - B_{22} \\ S_2 = A_{11} + A_{12} \\ S_3 = A_{21} + A_{22} \\ S_4 = B_{21} - B_{11} \\ S_5 = A_{11} + A_{22} \\ S_6 = B_{11} + B_{22} \\ S_7 = A_{12} - A_{22} \\ S_8 = B_{21} + B_{22} \\ S_9 = A_{11} - A_{21} \\ S_{10} = B_{11} + B_{12} \end{aligned} \]

递归地计算 \(7\) 个矩阵积 \(P_1, P_2, \cdots, P_7\)，每个矩阵 \(P_i\) 都是 \(\frac{n}{2} \times \frac{n}{2}\) 的。

\[ \begin{aligned} P_1 = A_{11} \cdot S_1 = A_{11} \cdot B_{12} - A_{11} \cdot B_{22} \\ P_2 = S_2 \cdot B_{22} = A_{11} \cdot B_{22} + A_{12} \cdot B_{22} \\ P_3 = S_3 \cdot B_{11} = A_{21} \cdot B_{11} + A_{22} \cdot B_{11} \\ P_4 = A_{22} \cdot S_4 = A_{22}\cdot B_{21} - A_{22} \cdot B_{11} \\ P_5 = S_5 \cdot S_6 = A_{11} \cdot B_{11} + A_{11} \cdot B_{22} + A_{22} \cdot B_{11} + A_{22} \cdot B_{22} \\ P_6 = S_7 \cdot S_8 = A_{12} \cdot B_{21} + A{12} \cdot B_{22} - A_{22} \cdot B_{21} - A_{22} \cdot B_{22} \\ P_7 = S_9 \cdot S_{10}= A_{11} \cdot B_{11} + A_{11} \cdot B_{12} - A_{21} \cdot B_{11} - A_{21} \cdot B_{12} \end{aligned} \]

注意，上述公式中只有中间一列需要计算。

通过 \(P_i\) 计算 \(C_{11}, C_{12}, C_{21}, C_{22}\)，花费时间 \(O(n^2)\) 。

\[ \begin{aligned} C_{11} = P_5 + P_4 - P_2 + P_6 \\ C_{12} = P_1 + P_2 \\ C_{21} = P_3 + P_4 \\ C_{22} = P_5 + P_1 - P_3 - P_7 \end{aligned} \]

综合可得如下递归式：

\[ T(n) = \begin{cases} O(1) & n = 1 \\ 7T(\frac{n}{2}) + O(n^2) & n >1 \end{cases} \]

进而求出时间复杂度为：\(T(n) = O(n^{log_{2}^{7}})\) 。

四、Strassen算法的代码实现

我们以 MNN 中关于 \(\textit{Strassen}\) 算法源码实现来学习：https://github.com/alibaba/MNN/blob/master/source/backend/cpu/compute/StrassenMatmulComputor.cpp 。

类 StrassenMatrixComputor 提供了 \(3\) 个 API 供调用：

API	说明
_generateTrivalMatMul(const Tensor* AT, const Tensor* BT, const Tensor* CT);	普通矩阵乘法计算
_generateMatMul(const Tensor* AT, const Tensor* BT, const Tensor* CT, int currentDepth)	Strassen算法的矩阵乘法
_generateMatMulConstB(const Tensor* AT, const Tensor* BT, const Tensor* CT, int currentDepth)	Strassen算法的矩阵乘法（和MatMul的区别在于内存Buffer是否允许复用)

我们以 _generateMatMul 为例来学习下 \(\textit{Strassen}\) 算法如何实现，可以分成如下几步：

第一步：使用Strassen算法收益判断

在矩阵操作中，因为需要对矩阵的维数进行扩展，涉及大量读写操作，这些读写操作都需要大量循环，如果读写次数超出使用 \(\textit{Strassen}\) 乘法的收益的话，就得不偿失了，那么就使用普通的矩阵乘法。

/* 
Compute the memory read / write cost for expand Matrix Mul need eSub*lSub*hSub*(1+1.0/CONVOLUTION_TILED_NUMBWR), Matrix Add/Sub need x*y*UNIT*3 (2 read 1 write) 
*/

float saveCost = (eSub * lSub * hSub) * (1.0f + 1.0f / CONVOLUTION_TILED_NUMBWR) - 4 * (eSub * lSub) * 3 - 7 * (eSub * hSub * 3); 
if (currentDepth >= mMaxDepth || e <= CONVOLUTION_TILED_NUMBWR || l % 2 != 0 || h % 2 != 0 || saveCost < 0.0f) 
{ 
	return _generateTrivialMatMul(AT, BT, CT); 
}

第二步：分块

将矩阵 \(A, B, C\) \(3\) 个矩阵都分成 \(4\) 块：

auto aStride = AT->stride(0); 
auto a11 = AT->host<float>() + 0 * aUnit * eSub + 0 * aStride * lSub; 
auto a12 = AT->host<float>() + 0 * aUnit * eSub + 1 * aStride * lSub; 
auto a21 = AT->host<float>() + 1 * aUnit * eSub + 0 * aStride * lSub; 
auto a22 = AT->host<float>() + 1 * aUnit * eSub + 1 * aStride * lSub; 
auto bStride = BT->stride(0); 
auto b11 = BT->host<float>() + 0 * bUnit * lSub + 0 * bStride * hSub; 
auto b12 = BT->host<float>() + 0 * bUnit * lSub + 1 * bStride * hSub; 
auto b21 = BT->host<float>() + 1 * bUnit * lSub + 0 * bStride * hSub; 
auto b22 = BT->host<float>() + 1 * bUnit * lSub + 1 * bStride * hSub; 
auto cStride = CT->stride(0); auto c11 = CT->host<float>() + 0 * aUnit * eSub + 0 * cStride * hSub; 
auto c12 = CT->host<float>() + 0 * aUnit * eSub + 1 * cStride * hSub; 
auto c21 = CT->host<float>() + 1 * aUnit * eSub + 0 * cStride * hSub; 
auto c22 = CT->host<float>() + 1 * aUnit * eSub + 1 * cStride * hSub;

第三步：分治和递归

\(\textit{Strassen}\) 算法核心就是分治思想。这一步可以写成下列所示伪代码：

1. If n = 1 Output A × B 
2. Else 
3. Compute A11,B11, . . . ,A22,B22 % by computing m = n/2 
4. P1 Strassen(A11,B12 - B22) 
5. P2 Strassen(A11 + A12,B22) 
6. P3 Strassen(A21 + A22,B11) 
7. P4 Strassen(A22,B21 - B11) 
8. P5 Strassen(A11 + A22,B11 + B22) 
9. P6 Strassen(A12 - A22,B21 + B22) 
10. P7 Strassen(A11 - A21,B11 + B12) 
11. C11 P5 + P4 - P2 + P6 
12. C12 P1 + P2 
13. C21 P3 + P4 
14. C22 P1 + P5 - P3 - P7 
15. Output C 
16. End If

例如其中的一步代码如下所示：

{ 
	// S1=A21+A22, T1=B12-B11, P5=S1T1 
	auto f = [a22, a21, b11, b12, xAddr, yAddr, eSub, lSub, hSub, aStride, bStride]() { 
	MNNMatrixAdd(xAddr, a21, a22, eSub * aUnit / 4, eSub * aUnit, aStride, aStride, lSub); 
	MNNMatrixSub(yAddr, b12, b11, lSub * bUnit / 4, lSub * bUnit, bStride, bStride, hSub); 
}; 

	mFunctions.emplace_back(f); 
	auto code = _generateMatMul(X.get(), Y.get(), C22.get(), currentDepth); 
	if (code != NO_ERROR) 
	{ 
		return code; 
	} 
}

递归执行，得到最终结果！

Updated By Long Luo at 19th, Aug. 2019 at Shenzhen.